时间复杂度
科普:
算法的时间复杂度是一个函数,它定性描述该算法的运行时间。算法的时间复杂度通常用大O符号表述,定义为T[n] = O(f(n))。大O表示法是一种特殊的表示法,指出了算法的速度有多快。
从快到慢列出常见5种大O运行时间:
O(log n):也叫对数时间,这样的算法包括二分查找;
O(n):也叫线性时间,这样的算法包括简单查找;
O(n * log n):这样的算法包括快速排序;
O(n2):这样的算法包括选择排序;
O(n! ):这样的算法包括旅行商问题的解决方案。
注意:
大O表示法指出了最糟情况下的运行时间;
算法的速度指的并非时间,而是操作数的增速;
谈论算法的速度时,我们说的是随着输入的增加,其运行时间将以什么样的速度增加;
算法的运行时间用大O表示法表示。
空间复杂度
科普
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度,记做S(n)=O(f(n))。
注意:
- 通常来说,只要算法不涉及到动态分配的空间以及递归、栈所需的空间,空间复杂度通常为0(1);
- 算法的空间复杂度并不是计算实际占用的空间,而是计算整个算法的辅助空间单元的个数,与问题的规模没有关系。
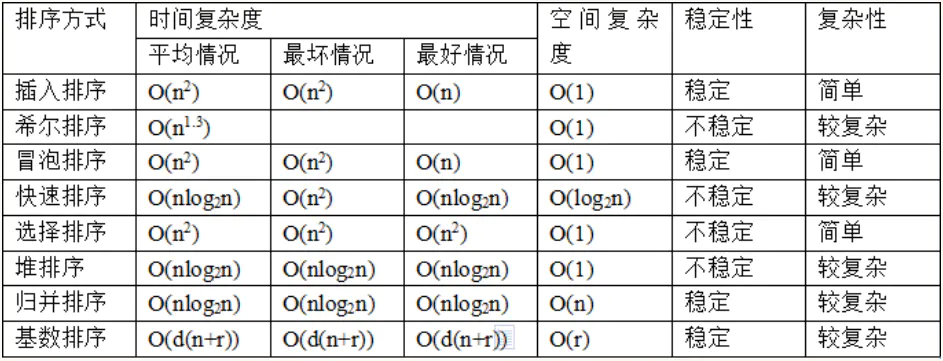
常见排序算法的时间复杂度和空间复杂度